QForm Microstructure (Grain size evolution)
QForm Grain size evolution is a special module for simulation of microstructure evolution during thermomechanical processing of steels, nickel-, titanium-, aluminum-based and other alloys.
 The main simulated processes:
The main simulated processes:
• Static recrystallization;
• Dynamic recrystallization;
• Metadynamic recrystallization;
• Normal grain growth;
• The coarsening of the microstructure.
The calculation takes into account the influence of temperature on the coefficients of the model as well as the cyclic recrystallization. The module can perform end-to-end calculation of microstructure evolution in the process chain with inheritance of calculation results and works for both 2D and 3D problems. The kinetics of recrystallization is described by the Johnson-Mehl-Avrami-Kolmogorov (JMAK) equation.
Both processor and postprocessor regimes of microstructure simulation are available in QForm.
The results of the calculation are shown in the workpiece fields. The following parameters are calculated: volume fraction and average grain size for dynamic, static and metadynamic recrystallization, total recrystallized volume fraction, average grain size, ASTM grain number, microstructure evolution type, retained strain, critical deformation, initial grain size before each recrystallization cycle, the number of completed recrystallizations when cyclic recrystallization calculation is enabled , as well as reference fields: deformation time, average temperature and strain rate during deformation, dwell time and grain growth time.

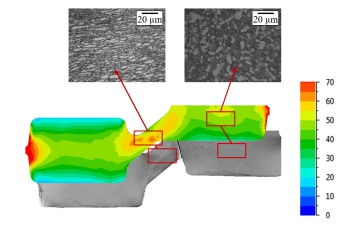
The module allows users to analyze and optimize technological processes of thermomechanical processing, including:
• Optimization of deformation mode parameters in order to obtain a regulated microstructure and the necessary operational properties;
• Selection of temperatures, the number and duration of dwell and heating stages to prevent grain growth and microstructure coarsening.
QForm also includes the MatILDa module developed by GMT mbH. This module can be used as an alternative for solving similar problems for steels and nickel alloys using the Sellars-Roberts model.